|
| নবম(৯ম) শ্রেণি গণিত অ্যাসাইনমেন্ট |
নবম(৯ম) শ্রেণি গণিত অ্যাসাইনমেন্ট ৪র্থ সপ্তাহ class 9 math assignment 4th week
শিরোনামঃ ২নং গণিত অ্যাসইনমেন্ট
আরো পড়ুনঃ
১ম সপ্তাহের সকল গ্রিড ও এ্যাসাইনমেন্ট প্রশ্ন ও সমাধান ২০২১ (৬ষ্ঠ থেকে ৯ম শ্রেণি)
আরো দেখুনঃ
- ৩য় সপ্তাহের (৯ম) নবম শ্রেণির কৃষি শিক্ষা এসাইনমেন্ট উত্তর ২০২১।
- ৩য় সপ্তাহ (৯ম) নবম শ্রেণির উচ্চতর গণিত অ্যাসাইনমেন্ট সমাধান ২০২১
- নবম (৯ম) শ্রেণির পৌরনীতি ও নাগরিকতা অ্যাসাইনমেন্ট উত্তর ২য় সপ্তাহ ২০২১
- ৫ম সপ্তাহের সকল অ্যাসইনমেন্ট দেখুন
- নবম শ্রেণি English অ্যাসাইনমেন্ট ৪র্থ সপ্তাহ
- নবম শ্রেণি রসায়ন অ্যাসাইনমেন্ট ৪র্থ সপ্তাহ
- ৪র্থ সপ্তাহের সকল শ্রেণির সকল অ্যাসাইনমেন্ট সমাধান দেখুন।
- নবম শ্রেণি ইতিহাস ও বিশ্বসভ্যতা অ্যাসাইনমেন্ট ৪র্থ সপ্তাহ।
নবম গণিত অ্যাসাইনমেন্ট ৪র্থ সপ্তাহের প্রম্নগুলো দেখুন এখানে
অ্যাসাইনমেন্ট শুরু
১ নং সৃজনশীল এর ‘ক’ প্রশ্নের উত্তর
দেওয়া আছে PQ = 3cm
এবং ∆PQR একটি সমবাহু ত্রিভূজ
১ নং সৃজনশীল এর ‘খ’ প্রশ্নের উত্তর
বিশেষ নির্বচনঃ ∆PQR একটি সমবাহু ত্রিভূজ। PS, QR এর উপর লম্ব। PS= ST আকিঁ। প্রমাণ করতে হবে যে, PQ+PR ﹥2PS
প্রমাণঃ ∆PQS ও ∆RST এর মধ্যে
PS = ST [ অঙ্কন অনুযায়ী]
QS = SR [PS, QR এর উপর লম্ব হওয়ায়]
এবং ∠PSQ = ∠RST [সমকোণ বলে]
সুতরাং ∆PQS ≅ ∆RST
∴ PQ = RT
∆PRT এ PR+RT﹥PT
বা, PR + PQ ﹥ PS+PT
বা, PR + PQ ﹥ PS+PS
বা, PR + PQ ﹥2PS (প্রমাণিত)
১ নং সৃজনশীল এর ‘গ’ প্রশ্নের উত্তর
বিশেষ নির্বচনঃ মনেকরি, ∆PQR একটি সমবাহু ত্রিভূজ। PS, QR এর উপর লম্ব। QS= SR, প্রমাণ করতে হবে যে, 4PS² = 3PR²
প্রমাণঃ ∆PQR একটি সমবাহু ত্রিভূজ হওয়ায়, PQ = QR = PR
QR = QS+SR
= SR + SR
= 2SR
এখন, ∆PRS এ PR² = PS² +SR²
বা, 4PR² = 4PS² +4SR²
বা, 4PR² = 4PS² +(2SR)²
বা, 4PR² = 4PS² +QR²
বা, 4PR² - QR² = 4PS²
বা,4PR² - PR² = 4PS²
বা, 3PR² = 4PS²
∴ 4PS² = 3PR² (প্রমাণিত)
২ নং সৃজনশীল এর ‘ক’ প্রশ্নের উত্তর
দেওয়া আছে, ∠P = 40⁰
এখানে, ∠D + ∠E + ∠F = 180⁰
বা, 40⁰ + ∠E + ∠F = 180⁰
বা, ∠E + ∠F = 180⁰ - 40⁰
বা, ∠E + ∠F = 140⁰
বা, 1/2 ∠E + 1/2 ∠F = 1/2× 140⁰
∴ 1/2 ∠E + 1/2 ∠F = 70⁰
এখান, ∠PEF+∠PFE + ∠EPF = 180⁰
বা, 1/2∠E+ 1/2 ∠F + ∠EPF = 180⁰
বা, 1/2∠E+ 1/2 ∠F + ∠EPF = 180⁰
বা, 70⁰ + ∠EPF = 180⁰
বা, ∠EPF = 180⁰ - 70⁰
∴ ∠EPF = 110⁰ (উত্তর)
২ নং সৃজনশীল এর ‘খ’ প্রশ্নের উত্তর
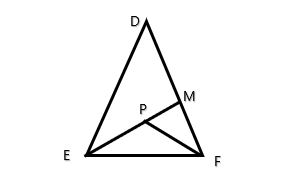
বিশেষ নির্বচনঃ মনেকরি, ∆ DEF এ DE﹥EF এবং বর্ধিত EP, DF কে M বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে যে, ∠DME স্থুলকোন।
প্রমাণঃ DE﹥EF হওয়ায়
∠F ﹥ ∠D
∠F + 1/2 ∠E ﹥ ∠D + 1/2 ∠E ------(i)
এখান, ∆ EDM এর বহিঃস্থ
∠EMF = ∠D + ∠DEM
= ∠D +1/2 ∠E
আবার, ∆ EMF বহিঃস্থ
∠DME = ∠F + ∠FEM
= ∠F +1/2 ∠E
উপরের মান (i) এ বসালে পাওয়া যাবে।
∠DME ﹥ ∠ EMF
চিত্র থেকে পাওয়া যায়
∠DME + ∠EMF = 1 সরলকোণ বা ২ সমাকোণ
∴ ∠DME ﹥ 90⁰
∴ ∠DME স্থুলকোন (প্রমাণিত)
২ নং সৃজনশীল এর ‘গ’ প্রশ্নের উত্তর
বিশেষ নির্বচনঃ মনেকরি, ∆ DEF এ ∠E ও ∠F বহিখণ্ডকদ্বয় Q বিন্দুতে মিলিত হয়েছে।
প্রমাণ করতে হবে যে, ∠EQF = 90⁰ - 1/2 ∠D
অঙ্কনঃ DE কে A পর্যন্ত এবং DF কে B পর্যন্ত বর্ধিত করি।
প্রমাণঃ ∆ DEF এ ∠D + ∠E +∠F = 180⁰
বা, 1/2∠D + 1/2∠E +1/2∠F = 1/2×180⁰
বা, 1/2∠D + 1/2∠E +1/2∠F = 90⁰
∆ DEF এ ∠EQF + ∠FEQ + ∠EFQ = 180⁰
বা, ∠EQF+1/2∠D+1/2∠F+1/2∠D+1/2∠E= 180⁰
বা, ∠EQF+1/2∠D+1/2∠E+1/2∠F+1/2∠D= 180⁰
বা, ∠EQF+90⁰ +1/2∠D= 180⁰
বা, ∠EQF= 180⁰ - 90⁰ -1/2∠D
বা, ∠EQF= 90⁰ - 1/2∠D
∴ ∠EQF= 90⁰ - 1/2∠D (প্রমাণিত)
১নং সংক্ষিপ্ত এর ‘১’ প্রশ্নের উত্তর
দেওয়া আছে, a-b = 4 এবং ab = 16
আমরা জানি, (a+b)² = (a - b)² +4ab
(a+b)² = 4² +4×16
(a+b)² = 16 +64
(a+b)² = 80
(a+b) = √80
(a+b) = √(16×5)
(a+b) = 4√5 (উত্তর)
১নং সংক্ষিপ্ত এর ‘২’ প্রশ্নের উত্তর
2 নং সংক্ষিপ্ত এর ‘৩’ প্রশ্নের উত্তর
a³-21a-20 এর উৎপাদক বিশ্লেষণ
a = -1 বসালে রাশিটির মান শূন্য হয় অর্থাৎ (a+1) রাশিটির একটি উৎপাদন
∴ a³-21a-20 = a³+a²-a²-a-20a-20
=a²(a+1) - a(a+1) -20(a+1)
= (a+1) (a²-a-20)
= (a+1) (a²-5a+4a-20)
= (a+1) {a(a-5) + 4(a-5)}
= (a+1) (a-5) (a-4)
১নং সংক্ষিপ্ত এর ‘৪’ প্রশ্নের উত্তর
মনে করি এখানে আসল P=X টাকা।
মুনাফার হার r = x% = X/100 টাকা
মুনাফা I = X টাকা
সময় n = 4 বছর
আমরা জানি,
I = Pnr
বা, X = X(X/100) × 4
বা, X = X²/25
বা, X²=25X
∴ X = 25 (উত্তর)
১নং সংক্ষিপ্ত এর ‘৫’ প্রশ্নের উত্তর
বা, P =5+4√5+4
∴ P = 9+4√5 (উত্তর)
৩ নং সৃজনশীল এর ‘ক’ প্রশ্নের উত্তর
দেওয়া আছে, m = 0
এবং a+b+c = m
বা, a+b+c = 0
বা, a+b = -c
বামপক্ষ, a³+b³+c³ -3abc
= (a+b)³ - 3ab(a+b) +c³-3abc
= (-c)³ - 3ab(-c) +c³ - 3abc
= -c³+3abc+c³-3abc
= 0
= ডানপক্ষ
∴a³+b³+c³ -3abc = 0 (প্রমাণিত)
৩ নং সৃজনশীল এর ‘খ’ প্রশ্নের উত্তর
দেওয়া আছে, c=0
এবং a+b+c = m
বা, a+b+0 = m
বা, a+b = m
আবার দেওয়া আছে, a²+b²+c² = n
বা, a²+b²+0² = n
বা, a²+b² = n
এবং a³+b³=p³
বামপক্ষ, = m³+2p³
= (a+b)³+2(a³+b³)
= a³+3a²b +3ab²+b³+2a³+2b³
= 3a³+3a²b +3ab²+3b³
= 3(a³+a²b +ab²+b³)
= 3{a²(a+b)+b²(a+b)}
= 3(a+b)(a²+b²)
= 3mn
= ডানপক্ষ
∴m³+2p³= 3mn (প্রমাণিত)
৩ নং সৃজনশীল এর ‘গ’ প্রশ্নের উত্তর
দেওয়া আছে, m=10
বা, a+b+c = m
বা, a+b+c = 10
এবং n=38
বা, a²+b²+c² = n
বা, a²+b²+c² = 38
আমরা জানি, (a+b+c)² = a²+b²+c² + 2(ab+bc+ca)
বা, (10)² = 38 + 2(ab+bc+ca)
বা, 100 = 38 + 2(ab+bc+ca)
বা, 2(ab+bc+ca) = 100-38
বা, (ab+bc+ca) = 62/2
∴ (ab+bc+ca) = 31
প্রদত্ত রাশি = (a-b)²+(b-c)²+(c-a)²
=a²-2ab+b²+b²-2bc+c²+c²-2ca+a²
=2a²+2b²+2c² -2ab-2bc-2ca
= 2×38 - 2×31
= 76 - 62
= 14 (উত্তর)
২নং সংক্ষিপ্ত এর ‘১’ প্রশ্নের উত্তর
উপাত্তসমূহের সর্বনিম্ন সংখ্যা 31 এবং পরিসর 90 হলে, সর্ব্বোচ্চ সংখ্যা হবে,
আমরা জানি, পরিসর = সর্ব্বোচ্চ সংখ্যা - সর্বনিম্ন সংখ্যা +১
বা, 90 = সর্ব্বোচ্চ সংখ্যা - 31+1
বা, 90 = সর্ব্বোচ্চ সংখ্যা -30
বা, 90+30 = সর্ব্বোচ্চ সংখ্যা
∴ সর্ব্বোচ্চ সংখ্যা = 120
২নং সংক্ষিপ্ত এর ‘২’ প্রশ্নের উত্তর
1 -- 22 পর্যন্ত 3 দ্বারা বিভাজ্য সংখ্যাগুলোর মধ্যক নির্ণয়ঃ
1 -- 22 পর্যন্ত 3 দ্বারা বিভাজ্য সংখ্যাগুলোর হলো ঃ 3, 6, 9, 12, 15, 18, 21
এখানে, n = 7 (বিজোড় সংখ্যা)
∴মধ্যক = (n+1)/2 তম পদ
= (7+1)/2 তম পদ
= 8/2 তম পদ
= 4 তম পদ
∴মধ্যক = 12 (উত্তর)
২নং সংক্ষিপ্ত এর ‘৩’ প্রশ্নের উত্তর
1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 সংখ্যাগুলোর গড় = (1+0+1+0+1+0+1+0+1+ 0+1)÷11
= 6÷11
= 0.5454 (উত্তর)
২নং সংক্ষিপ্ত এর ‘৪’ প্রশ্নের উত্তর
30 জন বালকের মোট ওজন = (30×52) কেজি
= 1560 কেজি
15 জন বালকের মোট ওজন = (15×40) কেজি
= 600 কেজি
45 জন শিক্ষার্থীর গড় ওজন = (1560+600)÷45
= 2160 ÷ 45
= 48 কেজি (উত্তর)
২নং সংক্ষিপ্ত এর ‘৫’ প্রশ্নের উত্তর
28, 30, 25, 27, 28, 25, 32 সংখ্যাগুলোর প্রচুরক নির্ণয়ঃ
পদত্ব সংখ্যাগুলোর মধ্যে সবচেয়ে বেশি সংখ্যক বার রয়েছে 25, 28
৪ নং সৃজনশীল এর ‘ক’ প্রশ্নের উত্তর
এখানে, L = মধ্যক শ্রেণির নিম্নসীমা
n = মোট গণসংখ্যা
Fc = মধ্যক শ্রেণির পূর্ববর্তী শ্রেণির যোজিত গণসংখ্যা
h = শ্রেণি ব্যাপ্তি
fm= মধ্যক শ্রেনির গণসংখ্যা
৪ নং সৃজনশীল এর ‘খ’ প্রশ্নের উত্তর
|
শ্রেণিব্যপ্তি |
শ্রেণিমধ্যমাণ
(xi) |
গণসংখ্যা
(fi) |
ধাপ
বিচ্যুতি (ui) |
গণসংখ্যার
ধাপ বিচ্যুতি (fiui) |
|
51
- 60 |
55.5 |
8 |
-2 |
-16 |
|
61-70 |
65.5 |
10 |
-1 |
-12 |
|
71-80 |
75.5 |
15 |
0 |
0 |
|
81-90 |
85.5 |
12 |
1 |
12 |
|
91-100 |
95.5 |
5 |
2 |
10 |
|
|
|
⅀fi= 50 |
|
⅀fiui = -4 |
এখানে a = 75.5
⅀fiui = -4
⅀fi = 50
h = 10
= 75.5 + (-40/50)×10
= 75.5 + (-0.08) × 10
= 75.5 - 0.8
= 74.7 (উত্তর)
৪ নং সৃজনশীল এর ‘গ’ প্রশ্নের উত্তর
|
শ্রেণিব্যপ্তি |
শ্রেণিমধ্যমাণ |
গণসংখ্যা |
|
51
- 60 |
55.5 |
8 |
|
61-70 |
65.5 |
10 |
|
71-80 |
75.5 |
15 |
|
81-90 |
85.5 |
12 |
|
91-100 |
95.5 |
5 |
|
|
|
মোট = ৫০ |
ছক কাগজে X অক্ষ বরাবর শ্রেণিব্যপ্তি এবং Y অক্ষ বরাবর গণসংখ্যা নিয়ে আয়তলেখ অঙ্কন করা হলো। যেখানে, X অক্ষে ১ ঘর = শ্রেণিব্যপ্তি ২ একক ধরে এবং Y অক্ষে ১ ঘর = গণসংখ্যার ১ একক।
আরো দেখুনঃ